
ts=15ms
sovraelongazione < 50%
egrad=0
Dall'ultima delle specifiche si ricava che il controllo deve avere un polo nell'origine, è opportuno quindi inserire nella rete anche uno zero.
Dalla prima specifica si ricava che la banda passante del sistema in catena chiusa deve essere circa
wb=3/(15e-3)=200 rad/sec
wt=0.7 wb=140 rad/sec
Dalla seconda delle specifiche si ricava che il margine di fase deve essere superiore a 30°
Il progetto del compensatore è riportato all'interno dell'M-file progettolevitatore.m
Inseriamo le funzioni di trasferimento ricavate:
» num=-5368.31
» den=[1 0 -864.39]
il diagramma di Bode relativo risulta essere:

aggiungiamo ora l'integratore con lo zero (compensatore PI) per soddisfare la terza specifica, utilizziamo anche uno zero il quale deve essere prima della frequenza di attraversamento.
» num1=conv(num,[1/0.5 1]);
» den1=conv(den,[1/0.5 0]);

Dal diagramma di Nyquist si nota che, avendo un polo instabile in catena aperta, è necessario incircolare il punto -1 in senso antiorario, ne segue che bisogna inserire un segno meno nella funzione di trasferimento in anello aperto.
» num2=-num1

In questa configurazione è possibile analizzare il diagramma di Bode per conoscere i termini in cui inserire la rete anticipatrice necessaria per la stabilizzazione del sistema in catena chiusa.

Dalla figura risulta evidente che nella frequenza scelta come attraversamento dell'asse a 0dB (wb=140 rad/sec), bisogna inserire una rete anticipatrice (derivativa) in grado di recuperare almeno 40°
» numc=[1/140 1];
» denc=[1/(4*140) 1];
I diagrammi di bode della rete anticipatrice sono riportati in figura:
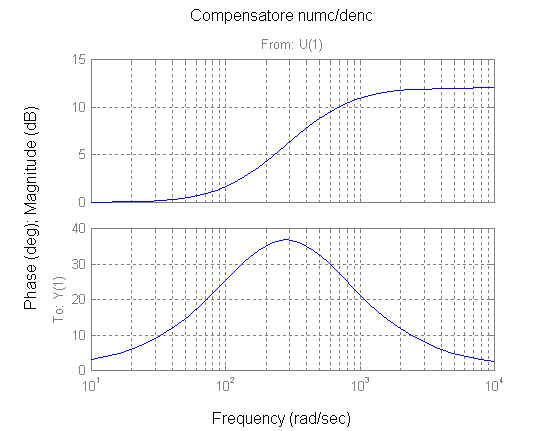
Utilizzando questo compensatore, è possibile andare a verificare l'andamento dei diagrammi di Bode e di Nyquist dell'impianto in serie al regolatore in catena aperta:
» [numca,denca]=series(numc,denc,num2,den1);
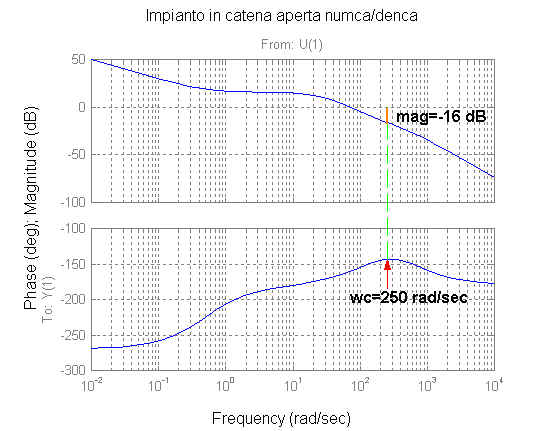

Dal diagramma di Nyquist si può notare che il punto -1 è incircolato una volta in senso antiorario, ne segue che il sistema in catena chiusa con retroazione unitaria risulta essere stabile.
Non resta ora da fare altro che variare il guadagno del compensatore in modo da ottenere il margine di fase desiderato ad una frequenza superiore a 140 rad/sec, così abbiamo a disposizione un maggiore margine di fase ed una banda più ampia. Quanto detto può essere ottenuto andando a variare il guadagno del compensatore, che si ripercuote in una traslazione verso l'alto del modulo del diagramma di Bode.
Per sapere di quanto deve essere aumentato il guadagno occorre conoscere il valore del modulo alla frequenza di 250 rad/sec (dove si ha il margine di fase massimo, leggermente superiore a 140 rad/sec):
» [mag,pha,w]=bode(numca,denca,250)
mag =
1.5833e-001
pha =
-1.4342e+002
w =
250
Alla frequenza di 250 rad/sec vi è un margine di fase di 37°, ma bisogna aumentare il guadagno kc di una quantità pari a
» kc=1/mag
E' ora possibile costruire il nuovo sistema in catena aperta:
» numca2=numca*kc;
i cui diagrammi di Bode e di Nyquist sono i seguenti:


Dai grafici è possibile verificare che il sistema è stabile in catena chiusa ed il margine di fase è superiore a quello richiesto.
Non rimane ora altro che verificare che il sistema in catena chiusa risponda alle richieste.
» [numcc,dencc]=cloop(numca2,denca);
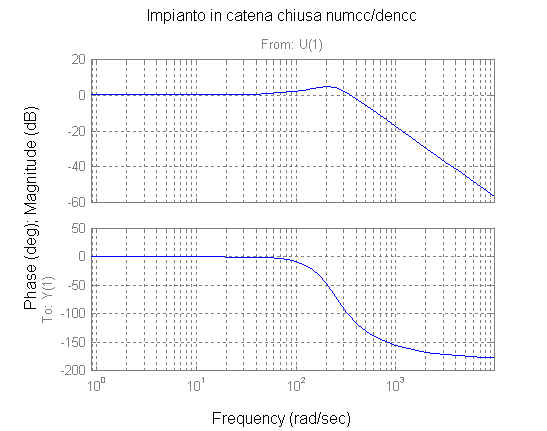

Dalla risposta al gradino e dal diagramma di Bode del modulo è possibile verificare che il sistema in catena chiusa ha un tempo di salita inferiore a 15 ms ed una sovraelongazione inferiore al 50%.
Il compensatore risultante del sistema risulta essere:
