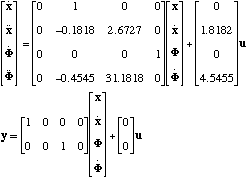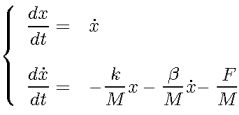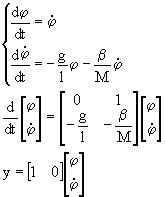- Usare il comando help ed in
particolare help plot, help semilogx, help
loglog, help grid.
- Trovare le radici del polinomio
x4+15x3+7x2+9x+4
- per via grafica
- per via analitica
Per fare ciˇ Ŕ necessario
seguire i seguenti passi:
- generare un vettore di x
- valutare il polinomio nei punti di x
(polyval)
- fare il grafico del polinomio (plot)
- trovare le intersezioni con
l’asse y=0
- utilizzare il comando roots
- Ricercare le radici dell’equazione
3x3+5x2+12x+12=x4+15x3+7x2+9x+4
- per via grafica
- per via analitica
Per fare ciˇ Ŕ necessario
seguire i seguenti passi:
- fare il grafico dei due membri
dell’equazione e trovare l’intersezione
- fare la sottrazione dei due polinomi
e trovare l’intersezione con l’asse y=0
- utilizzare il comando roots
- Caricare la matrice
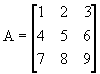
e provare ad invertirla.
Per fare ciˇ si possono usare i comandi:
- inv(A)
- A\I
Dove I Ŕ la matrice identitÓ che puˇ
essere creata con il comando I=eye(3)
- Si puˇ poi calcolare il determinante di A
che risulta essere 0. In questo modo Ŕ possibile
confrontarsi con alcuni dei problemi di carattere
numerico che si possono incontrare nell’uso di
Matlab
- Calcolare il polinomio caratteristico di A
- Calcolare gli autovalori di A e vedere che
questi siano uguali alle radici del polinomio
caratteristico di A.
- Caricare la matrice
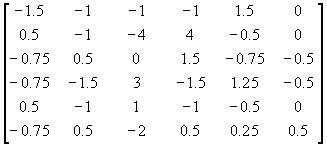
e provare a calcolare di questa matrice, molto
pi˙ grande, autovalori, autovettori e polinomio caratteristico.
Provare quindi, applicando una opportuna trasformazione, a
mettere la matrice in forma diagonale.
Prima parte
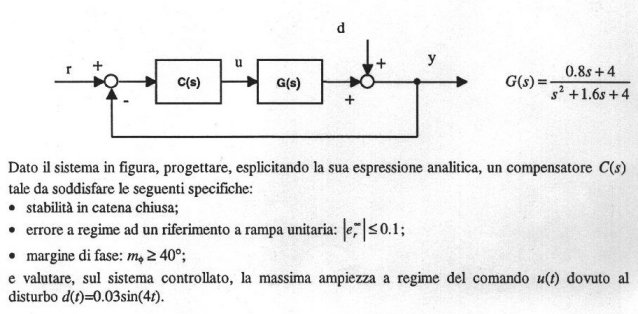
- Il sistema in figura rappresenta una
saldatrice a vibrazione nella quale un pezzo di materiale
plastico fissato superiormente viene fatto oscillare ad
una frequenza stabilita dall'utente e viene portato in
contatto con un pezzo inferiore. Losfregamento tra i due
pezzi provoca la saldatura degli stessi.
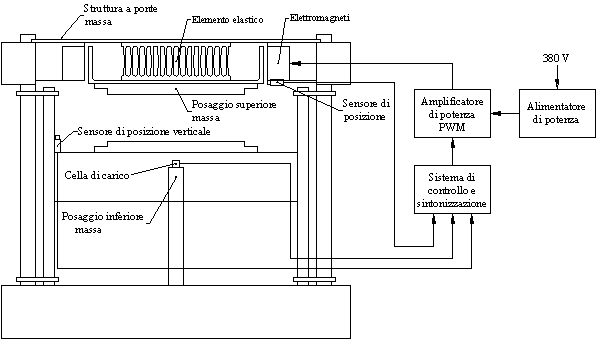
- L'intero sistema pu˛ essere modellizzato
come riportato in figura, dove la molla rappresenta
l'elemento elastico utilizzato per la vibrazione, mentre
lo smorzatore rappresenta lo smorzamento introdotto dalla
chiusura dei due pezzi tra loro.
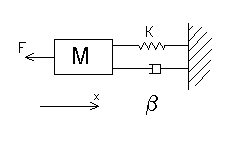
- Il modello meccanico della saldatrice,
come visto a esercitazione, ha le seguenti equazioni di
stato:
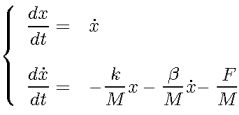
Dove:
M=10kg;
b=1kg/s;
k=5N/m;
- Se l’ingresso del sistema Ŕ la forza
F e l’uscita Ŕ la posizione x, scrivere le matrici
A, B, C, D del sistema.
- Sottoporre il sistema ad un ingresso
sinusoidale con frequenza pari a 70.71;
0.7071;0.07071rad/sec
- Calcolare il valore degli autovalori della
matrice A e visualizzare la loro posizione sul piano
complesso.
- Calcolare la risposta al gradino del
sistema
- Con b =30,1.414,0.01 calcolare:
Posizione degli autovalori (poli del
sistema)
Risposta al gradino e la frequenza di
oscillazione della risposta
- Con k=10,20,30 (b =5) calcolare:
Posizione degli autovalori (poli del
sistema)
Risposta al gradino e la frequenza di
oscillazione della risposta
- Dare una spiegazione di come varia la
posizione dei poli al variare di k e b
Seconda parte
- Dato il sistema visto ad esercitazione che
rappresenta il modello di una sospensione di automobile,
riportato in figura,
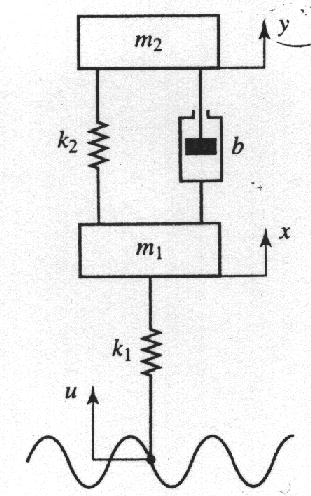
le cui equazioni di stato sono
le seguenti:
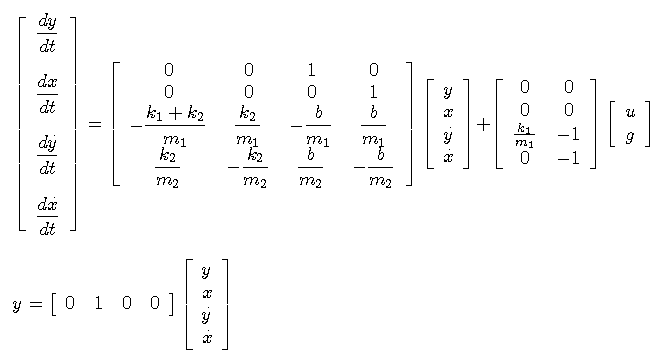
Dove:
m1=5kg;
m2=100kg;
k1=5N/m;
k2=20N/m;
b=50kg/s
- Progettare k2 e b in modo tale che il
sistema sottoposto ad un segnale di prova, relativo al
profilo stradale, abbia una escursione massima inferiore
a 4cm
- Il segnale di prova Ŕ di tipo sinusoidale
con frequenza 0.1862rad/sec ed ampiezza 1cm
- Inoltre i valori di k2 e b, devono
essere compresi tra 3<k2<20 e 0<b<50
- Provare a dare delle spiegazioni su cosa
avviene al sistema al variare della rigidezza
dell'ammortizzatore dello smorzamento introdotto dalla
sospensione.
Terza parte
- Disegnare la variazione della posizione
dei poli e degli zeri del sistema descritto dalla
seguente funzione di trasferimento al variare del valore
di K tra 0 e 50
(s+5)
--------------------
s^2+Ks+5K-4
- Disegnare la variazione della posizione
dei poli e degli zeri del sistema descritto dalla
seguente funzione di trasferimento al variare del valore
di K tra 0 e 3 e per ogni valore di k calcolare la
risposta al gradino
K(s+5)
--------------------
s^3+7s^2+(4-K)s+-2+5K
Per ognuna delle funzioni
di trasferimento sotto riportate, ricavare i coefficienti
di errori di posizione (Kp) con il Matlab e verificare i
risultati per via teorica.
5(s+1)
--------------
(s+2)(s+3)
2(s+5)
-----------
s^2+2s+5
96
--------------------------
4(2s+1)(3s+1)(4s+1)
4
----------
(s+3)
- Finire l’esercitazione precedente
- Studiare l’evoluzione nel tempo di un
sistema non lineare (il pendolo semplice) a partire da
diverse condizioni iniziali.
Allo scopo si ricorda che il pendolo semplice Ŕ retto
dalle seguenti equazioni
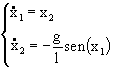
se non c’Ŕ smorzamento , altrimenti
le equazioni sono:
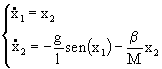
dove
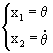
Dove q Ŕ l’angolo che il braccio del pendolo fa
rispetto alla posizione di riposo. Con l e M si sono indicate
rispettivamente la lunghezza e la massa del pendolo, mentre b rappresenta il
coefficiente di attrito viscoso.
- Linearizzare il sistema attorno alla
posizione di equilibrio e confrontare il comportamento
del sIstema non lineare con quello del sistema
linearizzato.
Per la linearizzazione, supponendo:
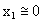
allora:
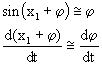
Se f Ŕ molto piccolo il sistema diventa:
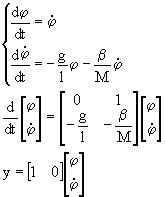
- Guardare il Demo di controllo,
dando il comando ‘ctrldemo’
- Disegnare i digrammi di Bode e calcolarne
i margini di fase e di guadagno per le seguenti funzioni
viste ad esercitazione:
s(s+100)
----------------
(s+1)(s+10)
100(s+10)^2
-----------------
s^2(s+100)
10s(s+1)
----------------
(s+10)(s+100)
100(s+10)
------------------------
s(s^2+80s+40000)
10(s-1)
-----------
(s+10)
- Disegnare i diagrammi di Bode (modulo e
fase) ed i diagrammi di Nyquist delle seguenti funzioni
di trasferimento
1
----------
(1+s/10)
s+10
-------------------
s(s+1)^2(s+100)
100(s+2)
--------------------
(s+1)^2(s+5)^2(s+10)
s+1
--------------------
s^2(s+2)(s+4)
- Analizzare la stabilitÓ dei sistemi
descritti dalle funzioni di trasferimento sopra
riportate, quando essi vengono chiusi con una retroazione
unitaria. Determinare margine di fase e margine di
guadagno.
- Considerare un sistema tempo-continuo ad
un ingresso ed un'uscita, la cui matrice A sia:
A=[-1.5 -1 1
-1 1.5;
0.5 -1 -4 4 -0.5;
-0.75 0.5 0 1.5 -0.75;
-0.75 -1.5 3 -1.5 1.25;
-0.75 0.5 -2 0.5 0.25];
che Ŕ la stessa vista nella prima
esercitazione. Si considerino, come vettori b e c', le colonne e le righe delle seguenti matrici B e C.
B=[0 -0.5 -1;
0 0.75 0.5;
-0.75 0.75 0.5;
0 1.5 1;
0 0.75 0.5];
C=[2 0 1 1 1;
-1 0 1 -1 1;
0 0 1 1 -1];
Provare ad analizzare la controllabilitÓ e
l'osservabilitÓ dei vari sistemi che cosý si ottengono,
valutando anche la possibilitÓ di realizzare, per ognuno di
essi, una retroazione degli stati misurati e/o osservati, tale
da:
- rendere stabile il sistema
- rendere stabile il sistema e garantire
che le coppie complesse coniugate degli autovalori
abbiano smorzamento >= 0.6
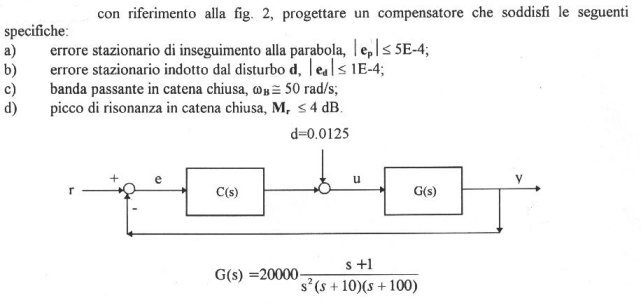
- Per il pendolo inverso riportato in figura
realizzare un controllo generico che stabilizzi il
sistema
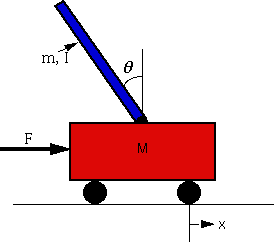
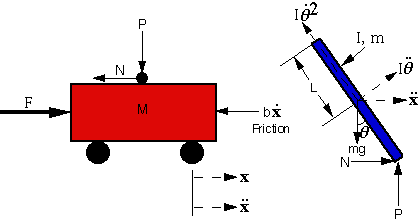
Le cui matrici di stato sono: