
| Il sistema treno | Diagramma di corpo libero e legge di Newton |
| Variabili di stato ed equazione dell’uscita | |
| Rappresentazione con Matlab |
Matlab può esser utilizzato per rappresentare un sistema fisico o un modello: per iniziare vediamo come puó essere possibile rappresentare un sistema fisico attraverso un insieme di equazioni differenziali.

In questo esempio ci occuperemo di un treno giocattolo costituito da una motrice e da un vagone. Assumendo che il treno possa viaggiare in una sola direzione, vogliamo applicare al treno un controllo in modo tale da avere una partenza ed un arresto dolci ed una marcia a velocità costante.
La massa della motrice e del vagone sono rappresentate da M1 e M2 rispettivamente: le due masse sono collegate da un gancio che supponiamo avere un coefficiente di rigidezza k. F rappresenta la forza applicata dalla motrice, mentre b rappresenta il coefficiente di attrito viscoso dovuto alle rotaie.
Il sistema puó essere rappresentato col seguente diagramma di corpo libero:
Dalla legge di Newton sappiamo che la somma delle forze agenti su una massa é eguale al prodotto della massa per la sua accelerazione. In questo caso le forze agenti su M1 sono quelle dovute al gancio, all’attrito e la forza applicata dalla motrice. Le forze agenti su M2 invece sono quelle dovute al gancio ed all’attrito. In direzione verticale la forza gravitazionale è equilibrata dalla reazione delle rotaie, per cui non c’è accelerazione in questa direzione.Le equazioni del moto in direzione orizzontale sono le seguenti:
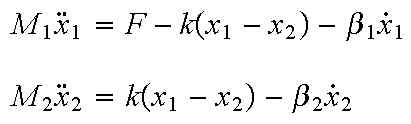
Questo sistema di equazioni può essere riscritto nella forma in variabili di stato. Assumendo come variabili di stato X1, X2, V1 V2 e come input la forza F, le equazioni in variabili di stato assumono questa forma:
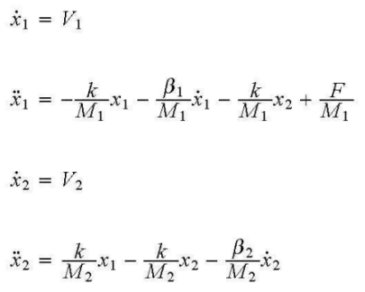
Se poi supponiamo che l’uscita del sistema sia la velocità della motrice, l’equazione di uscita sarà:
1. Funzione di trasferimento
Per ottenere la funzione di trasferimento del sistema è necessario innanzitutto calcolare la trasformata di Laplace delle equazioni scritte precedentemente. Usando queste equazioni è possibile ricavare la funzione di trasferimento Y(s)/F(s) in funzione di termini costanti, ottenendo questo risultato:
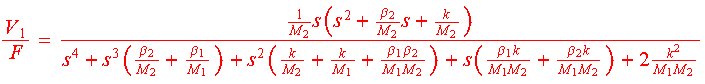
2. Spazio degli stati
Un altro metodo per risolvere il problema è utilizzare la forma dello spazio degli stati. Si caratterizza il sistema attraverso quattro matrici A, B, C e D attraverso le quali è possibile risolvere il problema; le matrici che si ottengono passando dalla forma in variabili di stato a quella in spazio degli stati sono riportate qui di seguito.
Vedremo ora come introdurre le equazioni precedentemente ricavate in un M-file di Matlab. Poiché Matlab non può manipolare variabili simboliche è necessario assegnare un valore numerico ad ognuna delle variabili, ad esempio:
- M1=1 kg
- M2=0.5 kg
- k=1 N/m
- F=1 N
- u=0.002 s/m
- g=9.8 m/s^2
Create ora un nuovo M-file ed introducete i seguenti comandi:
M1=1;
M2=0.5;
k=1;
F=1;
b1=0.02;
b2=0.01;
g=9.8;
Sono ora possibili 2 scelte per risolvere il problema: 1) Utilizzare la funzione di trasferimento, 2) Utilizzare la forma dello spazio degli stati. Se si sceglie di utilizzare la funzione di trasferimento, bisogna aggiungere al fondo dell’M-file appena creato i seguenti comandi:
num=1/M1*[1 b2/M2 k/M2 0];
den=[1 b2/M2+b1/M1 k/M2+k/M1+(b1*b2)/(M1*M2) (b1*k+b2*k)/(M1*M2) 2*k^2/(M1*M2)];
Se invece si sceglie la forma nello spazio degli stati bisogna aggiungere al fondo dell’M-file appena creato i seguenti comandi:
A=[0 1 0 0;-k/M1 -b1/M1 k/M1 0;0 0 0 1;k/M2 0 -k/M1 -b2/M2];
B=[0;1/M1;0;0];
C=[0 1 0 0];
D=[0];
La funzione calcola la risposta all’implulso di un sistema: ad esempio, volendo calcolare la risposta all’impulso di un sistema con funzione di trasferimento:
H(s)=(2s2+5s+1)/(s3+2s2+3s)
Basta fare:
» num=[2 5 1];
» den=[1 2 3 0];
» t=linspace(0,10,1000);
» plot(t,impulse(num,den,t));
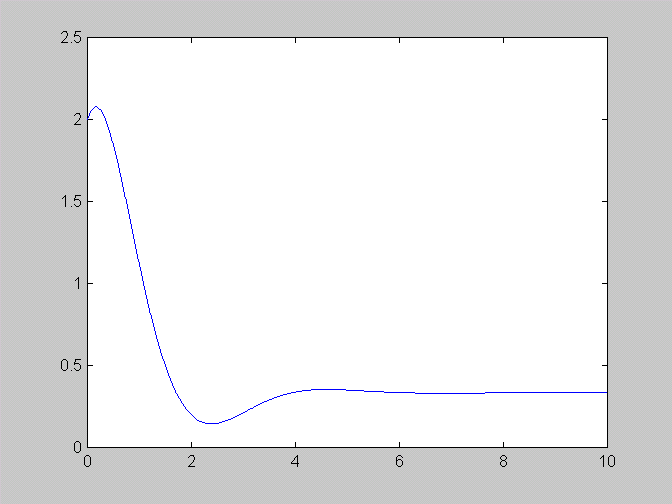
Calcola la risposta al gradino di un sistema. Ad es.
» step(A,B,C,D,IU,t);
Stampa la risposta al gradino di un sistema del tipo:
dx/dt=Ax+bu
y=Cx+Du
Cui sia stato applicato un ingresso a gradino.
La funzione lsim permette di ottenere una simulazione della risposta nel tempo di un sistema tempo invariante al quale è applicato un generico ingresso.
L'istruzione LSIM(A,B,C,D,U,T) fa il grafico della risposta nel tempo del sistema A,B,C,D sottposto all'ingresso dei segnali U,T.Il vettore dei tempi T, consiste in un vettore di elementi egualmente spaziati; U è una matrice con tante colonne quanti sono gli ingressi e la cui i-esima riga specifica i valori di ingresso ai tempi T(i).
t = 0:0.01:5; u = sin(t); lsim(A,B,C,D,u,t)
simula la risposta del sistema SYS all'ingresso u(t) = sin(t) la cui durata è di 5 sec.
Vedere l'help per ulteriori informazioni.