
| IL DIAGRAMMA DI NYQUIST | |||
| Il criterio di Cauchy | Stabilità ad anello chiuso | Margine di guadagno | Margine di fase |
Il metodo della risposta in frequenza è probabilmente meno intuitivo di altri metodi che avete studiato in precedenza, ma in effetti presenta alcuni vantaggi non indifferenti, specialmente quando si tratta di creare delle funzioni di trasferimento partendo da un sistema reale con le sue caratteristiche.
La risposta in frequenza di un sistema può essere studiata in due modi diversi: tramite il diagramma di Bode o tramite il diagramma di Nyquist. Entrambi i diagrammi visualizzano le medesime informazioni e la differenza consiste solo nel modo in cui queste vengono presentate.
La risposta in frequenza di un sistema rappresenta la sua risposta ad un ingresso sinusoidale al variare della frequenza dell’ingresso: la risposta di un sistema lineare ad un ingresso sinusoidale è a sua volta una sinusoide ma con diverse caratteristiche di ampiezza fase. La risposta in frequenza è definita come la differenza esistente in ampiezza e fase fra la sinusoide in ingresso e quella in uscita.
Per studiare la risposta in frequenza creiamo un vettore delle frequenze (che va da zero ad infinito) e calcoliamo il valore della funzione di trasferimento del sistema a quelle frequenze. Se G(s) è la funzione di trasferimento del sistema ad anello aperto e w è il vettore delle frequenze, noi plotteremo G(j*w) in funzione di w. Poiché G(j*w) è un numero complesso possiamo plottarne separatamente il modulo e la fase (diagramma di Bode) oppure la posizione sul piano complesso (diagramma di Nyquist).
Come descritto prima il diagramma di Bode è la rappresentazione in modulo e fase di G(j*w) (dove il vettore w contiene solo frequenze positive). Per vedere il diagramma di Bode di una funzione di trasferimento si può usare il comando:
» bode(50,[1 9 30 40])
che con questi valori inseriti traccia il diagramma di Bode della funzione di trasferimento:
50
-----------------------
s^3 + 9 s^2 + 30 s + 40

È bene notare gli assi del grafico: la frequenza è in scala logaritmica, la fase è espressa in gradi, l’ampiezza è espressa come guadagno in decibel.
E' possibile calcolare i diagrammi di Bode per valori di frequenza definiti utilizzando la seguente forma:
» w=logspace(-1,3,100); %calcola un vettore
di pulsazioni spaziate logaritmicamente
» bode(50,[1 9 30
40],w) %riporta
in figura il diagramma di Bode per le frequenze specificate
Se si vogliono utilizzare le potenzialità del comando plot per il diagramma di Bode è possibile usarle nel seguente modo:
» w=logspace(-1,3,100); %calcola un vettore
di pulsazioni spaziate logaritmicamente
» [mag,pha]=bode(50,[1
9 30 40],w) %riporta in figura il diagramma di Bode per le
frequenze specificate
»
subplot(211), semilogx(w,mag)
» subplot(212), semilogx(w,pha)
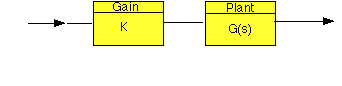
Supponiamo di avere questo sistema;
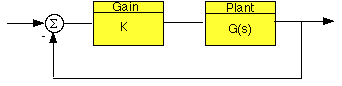
Dove k è un guadagno regolabile (costante) e G(s) è la funzione di trasferimento che stiamo considerando. Il margine di guadagno è definito come la variazione di guadagno k ad anello aperto necessario a rendere instabile il sistema. Sistemi con un grande margine di guadagno possono sopportare grandi variazioni nei parametri del sistema prima di diventare instabili ad anello chiuso.
Ricordate che un guadagno unitario in modulo è pari ad un guadagno zero espresso in dB.
Il margine di fase è definito come la variazione in differenza di fase ad anello aperto necessaria a rendere instabile il sistema.
Il margine di fase è dato dalla distanza fra la curva di fase e la linea a –180 deg alla frequenza in cui si ha un guadagno di zero dB (detta frequenza di crossover del guadagno, in inglese punto Wgc). Analogamente il margine di guadagno è dato dalla distanza fra la curva del modulo e la linea a zero dB alla frequenza in cui si ha una fase di –180deg (detta frequenza di crossover della fase, in inglese punto Wpc)

Un interessante vantaggio del margine di fase è che non è necessario plottare nuovamente il diagramma di Bode per calcolarne il nuovo valore dopo avere cambiato il guadagno del sistema: infatti aggiungere un guadagno ha il solo effetto di spostare verso l’alto il diagramma del modulo e ciò equivale ad un semplice spostamento dell’asse y. Calcolare il nuovo margine di fase si riduce quindi a cercare la nuova frequenza di incrocio con gli zero dB e leggere il relativo valore della fase.
Supponendo di avere digitato il comando:
» bode(50,[1 9 30 40]).
Si ottiene questo diagramma di Bode:
Si può vedere che il margine di fase è di circa 100°. Supponendo ora di aggiungere un guadagno di 100 e di calcolare il nuovo diagramma con il comando:
» bode(100*50,[1 9 30 40])
si ottiene questo grafico (notare che sono stati cambiati gli assi per mantenere la stessa scala dell’altro grafico: il grafico restituito normalmente potrebbe essere leggermente diverso):
Come si può vedere il diagramma della fase è esattamente lo stesso di prima , mentre quello del modulo è spostato verso l’alto di 40 dB (corrispondenti ad un guadagno di 100 in modulo). Il margine di fase è ora di circa –60deg: questo stesso risultato poteva essere ottenuto spostando verso il basso di 40 dB l’asse y del diagramma del modulo (potete provare a vedere questo sul primo grafico cercando l’intersezione con ila linea di –40 dB e leggendo il valore della fase).
Si possono calcolare i margini di guadagno e fase direttamente tramite il comando Matlab ‘margin’; questo comando restituisce i margini di guadagno e fase, le frequenze di crossover ed una rappresentazione grafica di queste grandezze sul diagramma di Bode. Ad esempio:
» margin(50,[1 9 30 40])

E' possibile conoscere in modo preciso il margine di fase e di guadagno andando a cercare sul vettore dei moduli o delle fasi il valore di frequenza che ha modulo a 0dB (per il margine di fase) oppure fase a 180deg (per il margine di guadagno). Per fare questo si può utilizzare l'istruzione find nel seguente modo:
»
[mag,pha,w]=bode(50,[1 9 30 40]); %calcola i valori di modulo e fase di
Bode il mag NON E' IN dB
» indexw0=find(mag<1.5 & mag>0.5); %cerca gli indici
dei valori di pulsazione in cui il guadagno è circa nullo
»
w0=w(indexw0) %inserisce in w0 la pulsazione di taglio
w0
=
1.7433e+000
» marginefase=180+pha(indexw0) %calcola il valore del margine di fase
marginefase
=
1.0506e+002
In modo analogo è possibile calcolare il margine di guadagno cercando quando la fase vale -180deg.
La larghezza di banda è definita come la frequenza alla quale il grafico del modulo del sistema ad anello chiuso vale –3 dB. In realtà però, dato che noi studiamo la risposta in frequenza di un sistema ad anello aperto per predirne il comportamento ad anello chiuso, si effettua generalmente una approssimazione del sistema del second’ordine e si assume come larghezza di banda la frequenza a cui il modulo della risposta ad anello aperto è compresa fra –6 e –7.5 dB, assumendo che la fase del sistema ad anello aperto sia compresa fra –135 e –225deg.
Per capire meglio l’importanza della larghezza di banda, vediamo come cambia l’uscita di un sistema al variare delle frequenze in entrata: troveremo che ingressi sinusoidali con frequenza minore della larghezza di banda sono restituiti in modo ragionevolmente buono, mentre ingressi a frequenza maggiore sono attenuati in ampiezza di un fattore 0.707 o maggiore (e sono anche molto sfasati rispetto all’ingresso).
Supponiamo di avere questa funzione di trasferimento ad anello chiuso per rappresentare un sistema:
1
---------------
s^2 + 0.5 s + 1
Innanzitutto calcoliamo la larghezza di banda guardando il diagramma di Bode;
» bode (1, [1 0.5 1 ])

Poiché questa è la funzione di trasferimento ad anello chiuso la larghezza di banda sarà il valore di frequenza a cui corrisponde un guadagno di –3 dB: guardando il grafico troviamo che corrisponde ad una frequenza di circa 1.4 rad/s.
Possiamo vedere che per una frequenza di input di 0.3 rad/s la sinusoide d’uscita ha ampiezza circa unitaria ed una fase spostata di pochi gradi rispetto all’ingresso. Ad una frequenza di 3rad/s invece l’ampiezza d’uscita vale circa –20dB (cioè 1/10 dell’ingresso e la fase è pressoché 180deg .
Possiamo ora usare il comando ‘lsim’ per simulare la risposta del sistema all’ingresso sinusoidale.
Per cominciare consideriamo un ingresso con frequenza minore della larghezza di banda; dobbiamo anche ricordare che a noi interessa la risposta a regime del sistema e pertanto dovremmo utilizzare degli assi opportuni per trascurare le fasi di transitorio.
» w= 0.3;
» num = 1;
» den = [1 0.5 1 ];
» t=0:0.1:100;
» u = sin(w*t);
» [y,x] = lsim(num,den,u,t);
» plot(t,y,t,u)
» axis([50,100,-2,2])
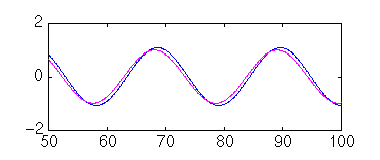
Notate che l’uscita (blu) segue l’input (viola ) piuttosto bene: è forse solo in ritardo di alcuni gradi.
Facciamo ora la stessa cosa con un ingresso di frequenza maggiore della larghezza di banda: troveremo una risposta molto diversa dall’ingresso originale:
» w = 3;
» num = 1;
» den = [1 0.5 1 ];
» t=0:0.1:100;
» u = sin(w*t);
» [y,x] = lsim(num,den,u,t);
» plot(t,y,t,u)
» axis([90, 100, -1, 1])
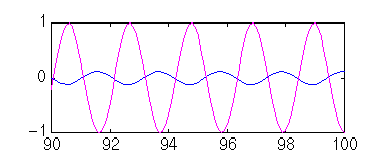
Nuovamente si può notare che l’ampiezza dell’uscita è circa 1/10 dell’ingresso ed è pressoché completamente fuori fase (in ritardo di 180 gradi). Potete provare a ripetere questo esperimento a frequenze diverse e controllare se i risultati corrispondono con quanto calcolate tramite il diagramma di Bode.
Il diagramma di Nyquist permette di studiare il comportamento e la stabilità di un sistema ad anello chiuso analizzando il suo comportamento ad anello aperto. Il criterio di Nyquist può essere utilizzato per il progetto del controllo, senza dover badare alla stabilità ad anello aperto (ricordate che il progetto con il metodo dei diagrammi di Bode assume che il sistema sia necessariamente stabile ad anello aperto). Perciò utilizziamo questo criterio per determinare la stabilità ad anello chiuso quando il diagramma di Bode ci fornisce informazioni non esaurienti. Vediamo ora di capire quali relazioni ci sono fra il diagramma di Bode e quello di Nyquist, attraverso una animazione.
Il diagramma di Nyquist è sostanzialmente una rappresentazione di G(j* w), dove G(s) è la funzione di trasferimento ad anello aperto e w è il vettore delle frequenze, che include l’intero semipiano destro: nel diagramma di Nyquist sono tenute in conto sia le frequenze positive che quelle negative (andando da zero all’infinito). Rappresenteremo le frequenze positive in rosso e quelle negative in verde. Il vettore delle frequenze utilizzato per il diagramma di Nyquist ha generalmente un aspetto di questo tipo (immaginando che il grafico passi per l’infinito):
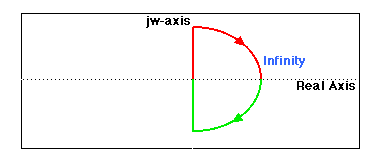
Se nel nostro sistema ci sono dei poli o degli zeri ad anello aperto sull’asse immaginario, la G(s) non sarà definita in questi punti ed è necessario passare attorno a questi punti quando si traccia il diagramma: tale diagramma potrebbe avere un aspetto di questo tipo:
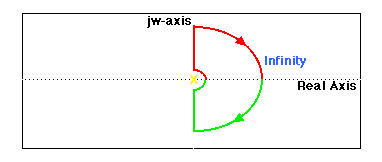
Si può notare che il contorno gira attorno al polo situato sull’asse immaginario. Come già suggerito il commando ‘nyquist’ non tiene in conto i poli e zeri situati sull’asse immaginario e pertanto produce un grafico scorretto.
Il criterio di Chauchy stabilisce che prendendo un contorno chiuso nel piano complesso e racchiudendo con questo le singolarità di una funzione complessa G(s), il numero di volte che il grafico di G(s) gira attorno all’origine è pari al numero di zeri di G(s) inclusi nel contorno delle frequenze meno il numero di poli di G(s) inclusi nel contorno delle frequenze. I giri attorno all’origine sono contati positivi se sono nella stessa direzione del contorno originale delle frequenze, negativi se sono in verso opposto.
Quando si studiano controlli a retroazione non si è interessati alla G(s) come funzione di trasferimento ad anello chiuso:
G(s)
---------
1 + G(s)
Se 1+G(s) incircola l’origine, allora G(s) incircola il punto –1. Poiché siamo interessati alla stabilità ad anello chiuso, vogliamo sapere se ci sono dei poli ad anello chiuso (zeri di 1+G(s)) nel semipiano destro.
Pertanto il comportamento del diagramma di Nyquist attorno al punto –1 sull’asse reale è molto importante: tuttavia gli assi utilizzati normalmente sul diagramma di Nyquist possono rendere difficoltoso vedere cosa succede attorno a questo punto.
Per vedere un semplice diagramma di Nyquist possiamo definire questa funzione di trasferimento:
0.5
-------
s - 0.5
e vederne il diagramma di Nyquist:
» nyquist (0.5,[1 -0.5])
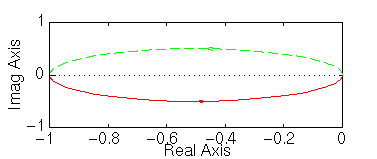
Considerate questo sistema con retroazione negativa:
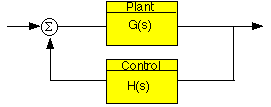
Ricordando dal criterio di Cauchy che il numero di volte N che il grafico di G(s)H(s) incircola il punto –1 è pari al numero di zeri Z di 1+G(s)H(s) racchiusi dal contorno delle frequenze meno il numero di poli P di 1+G(s)H(s) racchiusi dal contorno delle frequenze (N=Z-P). Tenendo conto delle funzioni di trasferimento ad anello aperto e ad anello chiuso e di numeratori e denominatori, si può vedere facilmente che:
Il criterio di Nyquist stabilisce poi che:
L’importante relazione che lega queste quantità è:
Z = P + N
Nota: questa è solo una convenzione per il criterio di Nyquist. Un’altra convenzione stabilisce che un N positivo conta gli incircolamenti antiorari, mentre P e Z restano le stesse. In questo caso la relazione diventa Z = P - N. In tutto questo tutorial verrà utilizzato il segno positivo per gli incircolamenti orari.
È molto importante imparare a contare il numero di volte che il diagramma gira attorno a –1. Un modo di vedere questo è immaginare di essere posti nel punto –1 e di seguire il diagramma dall’inizio alla fine. Bisogna ora chiedersi quante volte devo girarmi di 360 gradi completi? Di nuovo se la rotazione era oraria N è positivo, in caso contrario è da assumersi negativo.
Conoscendo il numero di poli (instabili) nel semipiano destro ed il numero di incircolamenti di –1 del diagramma di Nyquist, possiamo determinare la stabilità ad anello chiuso del sistema. Se Z = P + N è un numero positivo, diverso da zero il sistema ad anello chiuso è instabile.
Possiamo anche utilizzare il diagramma di Nyquist per trovare l’intervallo di valori del guadagno di un sistema a retroazione negativa unitaria che lo rendono stabile. Il sistema che utilizzeremo per le prove è di questo tipo:

Dove G(s) vale;
s^2 + 10 s + 24
- - - - - - - - - - - -
s^2 – 8 s + 15
questo sistema ha un guadagno variabile k che può essere variato per modificare la risposta del sistema ad anello chiuso: vedremo però che è possibile variare questo guadagno solo entro un certo limite, poiché dobbiamo verificare che il sistema ad anello chiuso sia stabile. Ciò che stiamo cercando in realtà è proprio questo: l’intervallo di valori di k tali per cui il sistema ad anello chiuso è stabile.
La prima cosa da calcolare è il numero dei poli positivi reali del sistema ad anello aperto:
» roots([1 -8 15])
ans =
5
3
I poli della funzione ad anello aperto sono entrambi positivi: perciò abbiamo bisogno di due incircolamenti antiorari del diagramma di Nyquist per avere un sistema ad anello chiuso stabile (Z = P + N). Se il numero degli incircolamenti è minore di due o sono in senso orario, il nostro sistema sarà instabile.
Vediamo ora il diagramma di Nyquist per un guadagno unitario:
» nyquist([ 1 10 24], [ 1 -8 15])
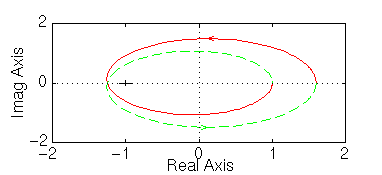
Ci sono due incircolamenti antiorari di –1: pertanto il sistema è stabile con guadagno unitario. Vediamo ora portando il guadagno a 20:
» nyquist(20*[ 1 10 24], [ 1 -8 15])
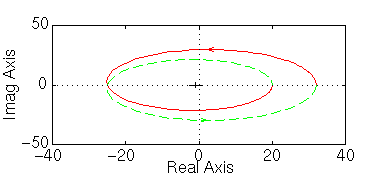
Il diagramma si è espanso: sappiamo perciò che il sistema sarà sempre stabile per quanto si aumenti il guadagno. Se invece diminuiamo il guadagno il diagramma si ridurrà ed il sistema potrebbe diventare instabile; vediamo ad esempio cosa succede con un guadagno di 0.5:
» nyquist(0.5*[ 1 10 24], [ 1 -8 15])
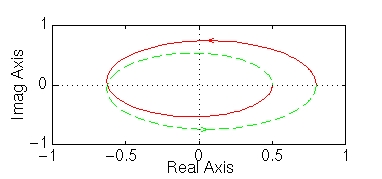
Il sistema è diventato instabile: procedendo per tentativi potremmo trovare che il sistema diventa instabile con un guadagno minore di 0.8. Potete controllare questo zoomando sull’origine dei diagrammi di Nyquist e plottando la risposta del sistema al gradino per i guadagni 0.79, 0.80, 0.81.
Abbiamo già definito il margine di guadagno come la variazione nel guadagno ad anello aperto espresso in dB necessario a 180 deg di sfasamento per rendere il sistema instabile: vedremo ora da dove viene questa definizione. Innanzitutto supponiamo di avere un sistema che sia stabile se non ci sono incircolamenti di –1, come:
50
- - - - - - - - - - - - - - - - -
s^3 + 9 s^2 +30 s + 40
Guardando le radici troviamo che non ci sono poli ad anello aperto nel semipiano destro e di conseguenza non ci sono incircolamenti di –1 nel diagramma di Nyquist. Per capire di quanto possiamo variare il guadagno prima di arrivare all’instabilità, possiamo guardare questa figura:
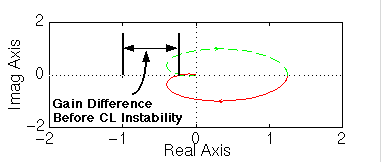
Il sistema ad anello aperto rappresentato in questo diagramma diventerà instabile ad anello chiuso se il guadagno viene incrementato di un certo valore: la zona dell’asse reale negativo compresa fra –1/a (definito come il punto a cui si ha un ritardo di fase di 180 deg, cioè dove il diagramma incrocia l’asse reale) e –1 rappresenta di quanto si può incrementare il guadagno prima di avere instabilità ad anello chiuso.
Possiamo quindi realizzare che se il guadagno è pari ad ‘a’ il diagramma toccherà il punto –1:
G(jw) = -1/a = a*G(jw) = a* -1/a => a*G(jw) = -1
Perciò diciamo che il margine di guadagno vale ‘a’ unità: abbiamo però detto precedentemente che il guadagno si misura abitualmente in dB. Il margine di guadagno sarà perciò:
GM = 20*log10(a) [dB]
Possiamo ora trovare il margine di guadagno della funzione di trasferimento stabile ad anello aperto che abbiamo visto prima. La funzione era:
50
- - - - - - - - - - - - - - - - -
s^3 + 9 s^2 +30 s + 40
ed il diagramma di Nyquist può essere trovato digitando:
» nyquist (50, [1 9 30 40 ])
per trovare il margine di fase abbiamo quindi bisogno di trovare esattamente il punto in cui c’è un ritardo di fase di 180 deg, per trovare il valore di ‘a’. Questo significa che la funzione di trasferimento in questo punto à reale (ha parte immaginaria nulla). Il numeratore è già reale, così dobbiamo occuparci del solo denominatore.
Quando s = j*w, i soli termini nel denominatore che avrebbero parte immaginaria sono quelli in potenza dispari di s; perciò, perché G(j*w) sia reale, deve essere:
-j w^3 + 30 j w = 0
che significa w=0 (questo è il punto più a destra sul diagramma di Nyquist) oppure w=sqrt(30). Possiamo calcolare il valore della funzione di trasferimento in questo punto con:
» polyval(50,j*w)/polyval([1 9 30 40],j*w)
ans =
-0.2174 + 0i
la parte immaginaria è nulla, cosa che verifica la nostra ipotesi.
Possiamo ora calcolare il margine di guadagno: avevamo trovato che la fase di 180 deg si trovava a -0.2174 + 0i, punto che avevamo definito precedentemente come ‘a’, che è proprio il valore cercato per il margine di guadagno. Volendo poi esprimere il guadagno in dB:
| -1/a = -0.2174 => a = 4.6 => GM = 20*log10( 4.6) = 13.26 dB |
Volendo verificare l’accuratezza di questo valore possiamo introdurre un guadagno di a=4.6 e zoomare sul diagramma di Nyquist:
» a = 4.6
» Nyquist(a*50,[1 9 30 40])
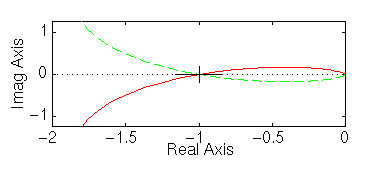
Il grafico passa proprio per il punto –1: potete ora verificare l’accuratezza del risultato zoomando sull’origine dei diagrammi di Nyquist e plottando la risposta del sistema al gradino per i guadagni 4.5, 4.6 e 4.7.
Abbiamo già parlato dell’importanza del margine di fase: vedremo ora dove ha origine questo concetto. Avevamo definito il margine di fase come la variazione nel ritardo di fase ad anello aperto necessaria a guadagno unitario a rendere instabile il sistema ad anello chiuso. Guardando questa figura possiamo visualizzare meglio il concetto:
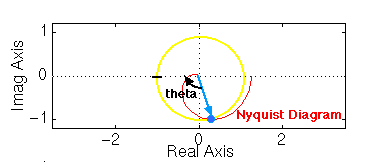
Sappiamo dall’esempio precedente che il sistema in questione diventa instabile ad anello chiuso se il diagramma di Nyquist incircola il punto –1. Vediamo quindi che se il grafico viene shiftato dell’angolo teta esso andrà a toccare il punto –1 sull’asse reale negativo, rendendo il sistema stabile marginalmente.
Perciò l’angolo necessario per rendere il sistema marginalmente stabile ad anello chiuso è chiamato margine di fase (misurato in gradi). Per trovare il punto da cui misurare questo angolo possiamo tracciare un cerchio di raggio unitario, trovando il punto nel diagramma di Nyquist con modulo unitario (guadagno di zero dB), e misurare lo spostamento di fase necessario per portare questo punto ad un angolo di –180 deg.
Questa istruzione produce la serie di due sistemi, il sistema risultante ha gli ingressi del sistema 1 e le uscite del sistema 2
» [A,B,C,D] = SERIES(A1,B1,C1,D1,A2,B2,C2,D2)
E' anche possibile, nel caso di sistemi a più ingressi e più uscite, connettere solo alcuni degli ingressi del sistema 2 ad alcune delle uscite del sistema 1, utilizzando la seguente istruzione:
» [A,B,C,D] = SERIES(A1,B1,C1,D1,A2,B2,C2,D2,OUTPUTS1,INPUTS2)
Analogamente a prima è possibile utilizzare la notazione in funzioni di trasferimento:
» [NUM,DEN] = SERIES(NUM1,DEN1,NUM2,DEN2)
La funzione cloop calcola la funzione di trasferimento del sistema in catena chiusa, con retroazione unitaria negativa (se non specificato diversamente) o positiva, a partire dalla funzione di trasferimento del sistema in catena aperta.

I possibili utilizzi sono i seguenti:
» [Ac,Bc,Cc,Dc] = CLOOP(A,B,C,D,SIGN)
dove SIGN definisce il segno della retroazione. Analogamente con funzioni di trasferimento:
» [NUMc,DENc] = CLOOP(NUM,DEN,SIGN)
Quando i sistemi utilizzati hanno più ingressi e più uscite è possibile definire la connessione utilizzando l'istruzione
» [Ac,Bc,Cc,Dc] = CLOOP(A,B,C,D,OUTPUTS,INPUTS)
dove OUTPUTS rappresentano le uscite del primo sistema ed INPUTS rappresentano gli ingressi utilizzati dal secondo sistema
Questa funzione connette in retroazione due sistemi generici come illustrati in figura:

L'istruzione viene utilizzata come segue:
» [A,B,C,D] = FEEDBACK(A1,B1,C1,D1,A2,B2,C2,D2,SIGN)
dove SIGN rappresenta, come in precedenza il segno della retroazione. E' possibile connettere tra loro sistemi con più ingressi e più uscite, specificando quali uscite del sistema 1 vengono connesse con gli ingressi del sistema 2:
» [A,B,C,D] = FEEDBACK(A1,B1,C1,D1,A2,B2,C2,D2,INPUTS1,OUTPUTS1)
E' possibile la connessione anche utilizzando la notazione con funzioni di trasferimento:
» [NUM,DEN] = FEEDBACK(NUM1,DEN1,NUM2,DEN2,SIGN)