La funzione pzmap, utilizzata nella forma
» pzmap(A,B,C,D)
oppure
» pzmap(num,den)
permette, dato un sistema SISO, di calcolarne gli zeri e poli e di tracciarne la posizione sul piano complesso tramite un grafico: i poli vengono rappresentati tramite delle ‘x’ e gli zeri tramite delle ‘o’. Nel caso di un sistema di tipo MIMO il comando plotta i poli e i transmission zeros del sistema.
Quando il comando viene digitato con degli argomenti a sinistra, nella forma:
» [P,Z]=pzmap(A,B,C,D)
i poli e gli zeri vengono memorizzati in vettori di nome P e Z e non viene tracciato il grafico.
Conversione dallo spazio degli stati alla funzione di trasferimento
Dalla funzione di trasferimento allo spazio degli stati
Un sistema dinamico è descritto per lo piú in uno di questi tre modi: tramite un sistema di equazioni nello spazio degli stati e le sue matrici corrispondenti, tramite una funzione di trasferimento con numeratore e denominatore in forma polinomiale oppure tramite una lista di zeri e poli con i relativi quadagni. Di volta in volta puó essere utile passare da una rappresentazione all’altra tramite Matlab.
Per iniziare supponiamo di avere un sistema di equazioni nello spazio degli stati e di volerlo convertire nella funzione di trasferimento equivalente: ció si puó fare con il comando:
» [num,den] = ss2tf(A,B,C,D,iu)
Questo comando crea il numeratore ed il denominatore della funzione di trasferimento relativa all’input iu-esimo; si puó notare che nella maggior parte degli esempi di questo tutorial è previsto un solo ingresso e perció non è necessario specificare il numero dell’ingresso.
Supponiamo ad esempio di avere questo sistema di equazioni differenziali:
Volendo trasformare questa rappresentazione in una funzione di trasferimento, è sufficiente far eseguire il seguente M-file
A = [0 1;0 -0.05];
B = [0;0.001];
C = [0 1];
D = 0;
[num,den]=ss2tf(A,B,C,D)
Matlab risponderá nella finestra di comando:
num =
0 0.0010 0
den =
1.0000 0.0500 0
che è il modo in cui Matlab memorizza la funzione di trasferimento:
0.001s + 0 F(s)= ------------------ s^2 + 0.05s + 0
Esistono alcune note di cui è bene tenere conto:
La funzione inversa della ss2tf è il comando tf2ss, che converte la funzione di trasferimento di un sistema nella corrispondente forma nello spazio degli stati. Il comando ha questa sintassi:
» [A,B,C,D] = tf2ss(num,den)
Una cosa importante da notare è che anche se un sistema è descritto da una singola funzione di trasferimento, esso pó essere equivalentemente descritto da diversi sistemi di equazioni nello spazio degli stati. Il comando tf2ss ne restituisce sempre uno ben preciso, quello relativo alla forma canonica di controllo: pertanto prendendo un sistema di equazioni nello spazio degli stati, trasformandolo in funzione di trasferimento e poi di nuovo nello spazio degli stati, non si ottiene piú il sistema iniziale, a meno che fosse giá inizialmente nella forma canonica di controllo.
Come esempio, prendiamo il numeratore ed il denominatore dell’esempio precedente e riconvertiamolo nello spazio degli stati. Otterremo:
» [A,B,C,D] = tf2ss(num,den)
A =
-0.1818 31.1818 4.4541 0
1.0000 0 0 0
0 1.0000 0 0
0 0 1.0000 0
B =
1
0
0
0
C =
0 1.8182 0 -44.5460
0 4.5455 0 0
D= 0
0
Si puó notare che questo non è piú il sistema iniziale, ma è una delle infinite rappresentazioni che si possono dare nello spazio degli stati di una data funzione di trasferimento, in particolare proprio quella che corrisponde alla forma canonica di controllo; bisogna peró notare che ora gli stati non hanno piú lo stesso significato che avevano originalmente.
Esiste anche un terzo modo di rappresentare un sistema dinamico, ed è la rappresentazione zero-poli; questa rappresentazione è sostanzialmente uguale a quella in funzione di trasferimento, solo che ora numeratore e denominatore sono fattorizzati in modo tale da avere tutti i poli a denominatore e tutti gli zeri a numeratore. Un formato normale di questo tipo di rappresentazione è ad esempio:
![]()
E’ bene ricordare che in una funzione di trasferimento propria il numero dei poli n è maggiore di quello degli zeri m. Matlab puó effettuare le trasformazioni sia dalla forma nello spazio degli stati sia da quella in funzione di trasferimento nella rappresentazione in zero-poli. I comandi relativi sono i seguenti:
»[z,p,k] = tf2zp(num,den);
»[z,p,k] = ss2zp(A,B,C,D,iu);
entrambi i comandi restituscono tre variabili: z, p, k. La variabile z restituisce tutti gli zeri in colonne, essendoci una colonna per ogni riga nel numeratore della funzione di trasferimento, ovvero per ogni uscita y (riga nella matrice C). La variabile p restituisce un vettore colonna contenente tutti i poli, la k un vettore colonna con i valori dei guadagni; le colonne dovrebbero avere tante righe quante sono le righe del numeratore, ovvero le uscite y. Per esempio si puó provare ad immettere il seguente M-file:
num = [1.8182 0 -44.5460;4.5455 -7.4373 0];
den = [1 0.1818 -31.1818 6.4786 0];
[z,p,k] = tf2zp(num,den)
oppure l’M-file:
A = [0 1 0 0;0 -0.1818 2.6727 0;0 0 0 1;0 -4.545 31.1818 0];
B = [0;1.8182;0;4.5455];
C = [1 0 0 0;0 0 1 0];
D = [0;0];
[z,p,k]=ss2zp(A,B,C,D,1)
ed otterremo questa risposta
z =
4.9498 1.6362
-4.9498 0
p =
0
0.2083
-5.7753
5.3851
k =
1.8182
4.5455
Correttamente, essendoci due colonne di zeri, il vettore k ha due righe, una per ogni colonna di z.
Naturalmente è possibile effettuare anche le trasformazioni inverse, tramite ad esempio il comando:
» [A,B,C,D] = zp2tf(z,p,k)
Analogamente a quanto gia descritto, anche in questo caso la rappresentazione nello spazio degli stati fornita da Matlab è quella relativa alla forma canonica di controllo; quindi, prendendo ad esempio le matrici z, p, k appena generate e riconvertendole nello spazio degli stati, otterremo:
» [A,B,C,D] = zp2tf(z,p,k)
A = -0.1818 31.1818 -6.4786 0
1.0000 0 0 0
0 1.0000 0 0
0 0 1.0000 0
B = 1
0
0
0
C = 0 1.8182 0 -44.5460
0 4.5455 -7.4373 0
D = 0
0
Si puó vedere che questo è lo stesso sistema di matrici che avevamo ottenuto con il comando tf2ss. Per effettuare invece la trasformazione nella forma di funzione di trasferimanto si puó usare:
» [num,den] = zp2tf(z,p,k)
Trasformando ad esempio le matrici z, p, k prima calcolate otterremo;
num = 0 0 1.8182 0 -44.5460
0 0 4.5455 -7.4373 0
den = 1.0000 0.1818 -31.1818 6.4786 0
che è la stessa funzione di trasferimento di partenza.
Il comando lsim è piuttosto simile al comando step (in effetti il comando step è un caso particolare di lsim); dato un sistema raprresentato nello spazio degli stati o in funzione di trasferimento, il comando lsim permette di simularne il comportamento applicando ingressi e condizioni iniziali arbitrarie.
Il comando
» lsim(A,B,C,D,U,T,X0)
crea la risposta nel tempo del sistema lineare:
. x = Ax + Bu y = Cx + Du
Le equazioni differenziali vengono integrate dall’istante T(0) all’istante T(lunghezza(T)), partendo dalla condizione iniziale X0 e usando l’input U. Il vettore dell’ input deve avere lo stesso numero di elementi del vettore T; se le condizioni iniziali sono tutte nulle, il vettore X0 puó essere omesso.
Supponiamo di avere un sistema descritto dalle suddette equazioni, essendo le matrici A, B ,C ,D:
A = [-20 -40 -60;1 0 0;0 1 0];
B = [1;0;0];
C = [0 0 1];
D=0;
Come si puó vedere dalle dimensioni delle matrici, il sistema ha tre stati, un entrata ed una uscita. Supponiamo di volere vedere la risposta del sistema con condizioni iniziali diverse da zero ed ingresso nullo: ció si puó fare in questo modo:
» T = 0:0.01:10; %definisce
l'intervallo di tempo
» U = zeros(size(T)); %definisce l'ingresso del sistema a zero
» X0 = [0.1 0.1 0.1]; %definisce le condizioni iniziali degli stati
» lsim(A, B, C, D, U, T, X0) %simula a disegna le risposte
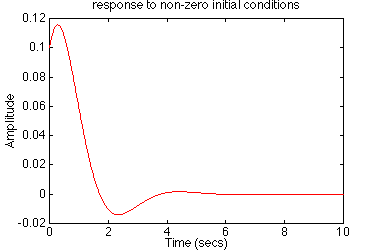
Quando il comando lsim viene appicato con degli argomenti sulla sinistra, ad esempio cosí:
» [Y, X] = lsim(A,B,C,D,U,T);
Matlab restituisce l’andamento degli stati e dell’uscita nelle matrici X e Y rispettivamente, ma non viene tracciato alcun grafico; la matrice Y ha tante colonne quante sono le uscite e tante righe quanti sono gli elementi di T.
Possiamo ora provare a calcolare la risposta al gradino utilizzando il comando lsim, creando un opportuno vettore dell’ingresso.
» T = 0:0.01:10;
» U = ones(size(T));
» [Y, X] = lsim(A,B,C,D,U,T);
» plot(T, Y)
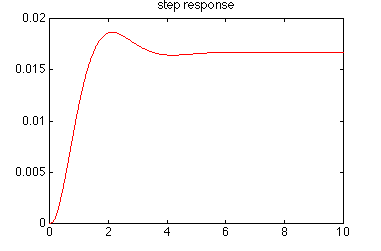
Analogamente possiamo vedere la risposta ad un ingresso sinusoidale, ad esempio del tipo:
u(t) = 0.1 sin(5t+1)
Ció si puó fare in questo modo;
» T = 0:0.01:10;
» U = 0.1*sin(5*T+1);
» [Y, X] = lsim(A,B,C,D,U,T);
» plot(T, Y)
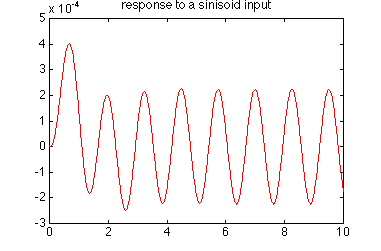
E’ bene ricordare che la risposta a regime di un sistema lineare soottoposto ad un ingresso sinusoidale è sempre a sua volta sinusoidale con pari frequenza ma diversa ampiezza e fase. La stessa risposta sinusoidale si poteva ottenere passando alla rappresentazione in funzione di trasferimento:
» T = 0:0.01:10;
» U = 0.1*sin(5*T+1);
» [num,den]=ss2tf(A,B,C,D);
» lsim(num,den,U,T)
Come prevedibile si ottiene lo stesso grafico di prima: poiché una funzione di trasferimento puó essere rappresentata da diversi sistemi di equazioni in variabili di strato, è possibile simulare un sistema in funzione di trasferimento solo con condizioni iniziali nulle.
La funzione step permette di calcolare la risposta al gradino di un sistema rappresentato tramite funzione di trasferimento o nello spazio degli stati. Un input a gradino può essere visto come un input che ha valore finito costante per tutti gli istanti di tempo positivi e valore nullo in tutti gli altri istanti; questo valore finito viene assunto di default pari a uno (l’input va da zero a uno nell’istante zero).
La sintassi del comando, a seconda del modo in cui è rappresentato il sistema è:
» step(A,B,C,D)
oppure
» step(num,den)
Il comando produrrà nello stesso grafico la risposta al gradino delle diverse combinazioni di ingresso-uscita.
Supponiamo di voler studiare un sistema meccanico caratterizzato da due stati, posizione e velocità, e che sia rappresentato nello spazio degli stati dalle seguenti matrici:
A = [0 1
0 -.05];
B= [0
0.001];
C = [1 0
0 1];
D = [0
0];
Il gradino in ingresso rappresenta in questo caso un cambiamento della forza agente sul sistema da un valore di 0 Newton al valore 1 Newton; questo sistema di equazioni di stato ha due uscite ed una entrata, pertanto nel grafico restituito dal comando saranno presenti due andamenti, uno per ogni uscita.
Per vedere questa risposta possiamo digitare:
» step(A,B,C,D)
Il comando step può anche essere utilizzato per sistemi che hanno più di un ingresso, utilizzando questa sintassi:
» step(A,B,C,D,iu)
In questo modo verrà creato un grafico in cui sono plottati gli andamenti delle uscite dovuti ad un gradino applicato all’ingresso iu-esimo. Analogo è il funzionamento del comando se il sistema è rappresentato da un funzione di trasferimento, con la sola eccezione che ora l’input è necessariamente unico e pertanto tutte le uscite saranno plottate assieme.
Possiamo ad esempio provare a trasformare il sistema in variabili di stato di prima, in funzione di trasferimento e verificare che si ottiene lo stesso grafico.
» [num,den]=ss2tf(A,B,C,D)
» step(num,den)
Nel caso si voglia simulare l’aplicazione di un ingresso a gradino non unitario è sufficiente moltiplicare le matrici B e D (o il numeratore della funzione di trasferimento) per il valore dell’altezza del gradino: ad esempio volendo simulare un gradino di ampiezza 100 è sufficiente utilizzare il comando:
» step(A,100*B,C,100*D,1)
oppure
» step(100*num,den)
con i quali otteniamo gli stessi andamenti di prima ad eccezione dei valori presenti sulla scala dell’asse y.
Queste risposte al gradino possono essere visualizzate secondo una scala dei tempi definita dall’utente: è necessario a questo scopo creare un vettore dei tempi che specifichi l’intervallo nel quale viene calcolata la risposta: se ad esempio ci interessa vedere la risposta di un sistema nei primi 80 secondi dall’applicazione del gradino, la sintassi del comando sarà:
» t=0:0.1:80;
» step(A,B,C,D,iu,t)
oppure
» step (num,den,t)
per il sistema in varibili di stato od in funzione di trasferimento rispettivamente.
Per concludere è possibile memorizzare l’andamento della risposta tramite l’indicazione di un argomento alla sinistra del comando, con la seguente sintassi:
» [y,x] = step(A,B,C,D,iu,t)
oppure
» [y,x] = step(num,den,t);
nel caso il vettore dei tempi fosse già stato specificato dall’utente,
» [y,x,t] = step(A,B,C,D,iu)
oppure
» [y,x,t] = step(num,den);
nel caso il vettore di tempi non sia conosciuto; il vettore y conterrà l’andamento della risposta, il vettore x l’andamento degli stati; in questo caso non viene effettuato il plottaggio del grafico.
Integra numericamente un insieme di equazioni differenziali ordinarie usando il metodo di Runge-Kutta di ordine 2 e 3. Es:
[t,x]=ode23(‘xprimo’,t0,tfinale,xo,tol1);
integra il sistema di equazioni differenziali definito nel file xprimo .m sull’intervallo temporale da to a tifinale con condizione iniziale xo, garantendo l’accuratezza tol1 per la soluzione ottenuta.
La variabile t è un vettore colonna contenente gli istanti di integrazione , mentre x è una matrice la cui m-esima riga contiene i valori delle variabili del sistema di equazioni nel m-esimo istante temporale precisato in t (si veda anche il comando ode memo).
Es.: si integri numericamente il sistema di equazioni differenziali ordinarie
dx1/dt=x2
dx2/dt=x2*(1-(x1)2)-x1
sull’intervallo temporale [0,20] con condizioni iniziali nulle.
Si puó integrare il sistema nel modo seguente:
t0=0; % istante iniziale
tfinale =20 % istante finale
x0=[0,0] % condizione iniziale
tol=1e-3 % tolleranza
[t,x]=ode23(‘xprimo’,t0,tfinale,xo,tol1);
dove il file xprimo.m contiene la seguente definizione del sistema di equazioni differenziali:
function xdot=xprimo(t,x)
xdot(1,1)=x(2);
xdot(2,1)=x(2)*(1-x(1)^2)-x(1)
Si osservi che nel file xprimo.m la variabile t costituisce il generico istante d’integrazione ed è uno scalare il cui valore è determinato dalla ode23 in modo da garantire l’accuratezza tol desiderata. La variabile t restituita dal comando ode23 contiene invece tutti gli istanti d’integrazione utilizzati ed è quindi un vettore la cui dimensione è pari al numero di volte in cui il comando ode23 ha richiamato internamente il file xprimo.m per calcolare la soluzione.