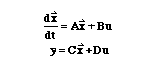
Ci sono molti modi diversi per descrivere un sistema di equazioni differenziali lineari. La rappresentazione nello spazio degli stati è data dalle equazioni:
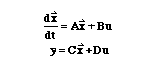
Dove x è un vettore di dimensioni n per 1 che rappresenta gli stati, u è uno scalare che rappresenta l’ingresso e y è uno scalare che rappresenta l’uscita. Le matrici A (n per n), B (n per 1) e C (1 per n) determinano le relazioni fra gli stati e le variabili di ingresso ed uscita. Notate che ci sono n equazioni differenziali del prim’ordine.
La rappresentazione nello spazio degli stati può anche essere utilizzata per rappresentare sistemi con ingressi ed uscite multipli (sistemi MIMO), ma in questo tutorial utilizzeremo solo sistemi a singolo ingresso e singola uscita (sistemi SISO).
Per vedere i nostri esempi utilizzeremo un sistema costituito da una sfera sospesa magneticamente: la corrente che passa attraverso i conduttori genera una forza elettromagnetica che può bilanciare la forza di gravità e che fa si che la sfera resti sospesa a mezz’aria.
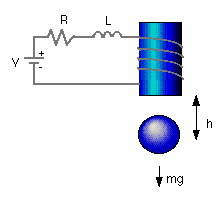
Il modello di questo sistema è stato definito in molti libri di controlli. Le equazioni per il sistema sono date da:
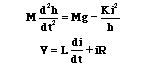
Dove h è la posizione verticale della sfera, i è la corrente che attraversa l’elettromagnete, V è la tensione applicata, M è la massa della sfera, g è la costante gravitazionale, L è l’induttanza, R la resistenza e K è un coefficiente che determina la forza magnetica esercitata sulla sfera.
Per semplicità sceglieremo i valori M = 0.05 Kg, K = 0.0001, L = 0.01 H, R = 1 Ohm, g = 9.81 m/sec^2 . Il sistema è in equilibrio (la sfera resta sospesa in aria) per h = K i^2/Mg (punto in cui dh/dt = 0). Linearizzando le equazioni nell’intorno del punto h = 0.01 m (dove la corrente nominale è circa 7 amp) otteniamo:
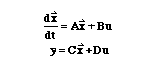
dove
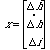
è il sistema di variabili di stato per il sistema (è un vettore 3 x 1), u è il voltaggio in entrata (delta V), e y (l’uscita), è il delta h. Possiamo ora introdurre le matrici in un M-file:
A = [ 0 1 0
980 0 -2.8
0 0 -100];
B = [0
0
100];
C = [1 0 0];
Una delle prime cose da fare con le equazioni di stato è trovare i poli del sistema: questi sono i valori di s per i quali det(sI - A) = 0, o gli autovalori della matrice A:
poles = eig(A) poles = 31.3050 -31.3050 -100.0000
Uno dei poli è nel semipiano destro, il che significa che il sistema è instabile ad anello aperto. Per vedere cosa succede a questo sistema instabile quando ci sono condizioni iniziali non nulle, aggiungete queste righe di comandi al vostro M-file:
t = 0:0.01:2; u = 0*t; x0 = [0.005 0 0]; [y,x] = lsim(A,B,C,0,u,t,x0); h = x(:,2); %Delta-h is the output of interest plot(t,h)
e fate eseguire il file nuovamente:
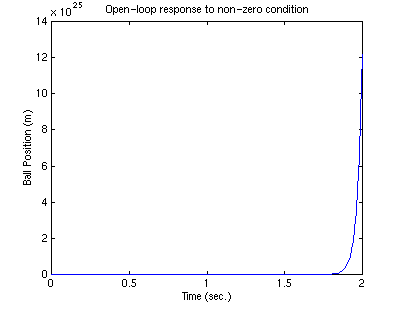
Sembra che la distanza fra la sfera e l’elettromagnete debba andare ad infinito, ma più probabilmente la sfera finisce prima sul tavolo o sul pavimento (e sicuramente va fuori dall’intervallo in cui la linearizzazione è valida).
Realizzazione di controlli mediante il posizionamento dei poli
Costruiamo ora un controllo per questo sistema. Lo schema di un sistema con retroazione sugli stati è il seguente:
Ricordate che il polinomio caratteristico per questo sistema ad anello chiuso è il determinante di (sI-(A-BK)). Poiché le matrici A e B*K sono tutte matrici di dimensioni 3 per 3 ci saranno tre poli per il sistema. Usando una retroazione degli stati possiamo posizionare i poli ovunque noi vogliamo. A questo scopo possiamo utilizzare la funzione Matlab place per trovare la matrice di controllo K, che ci permetterà di posizionare i poli dove desideriamo.
Per applicare questo metodo dobbiamo decidere dove vogliamo posizionare i poli del sistema ad anello chiuso: supponendo che i nostri criteri per il controllo siano di avere un tempo di assestamento <0.5 sec ed un overshoot <5%, possiamo provare a posizionare i due poli dominanti in -10 +/- 10i (con zeta = 0.7 o 45 gradi con sigma = 10 > 4.6*2).
Il terzo polo invece possiamo metterlo come tentativo a –50 e cambiarlo in seguito a seconda del comportamento che otteniamo dal sistema. Potete quindi ora rimuovere il comando lsim e tutto ciò che segue dal vostro M-file e sostituirvi queste linee di comandi:
p1 = -10 + 10i; p2 = -10 - 10i; p3 = -50; K = place(A,B,[p1 p2 p3]); lsim(A-B*K,B,C,0,u,t,x0);
Come si può vedere l’overshoot è troppo grande (ci sono anche degli zeri nella funzione di trasferimento che possono incrementare l’overshoot; nella formulazione in variabili di stato però non è possibile vederli). Proviamo a posizionare i poli più a sinistra e vediamo se le caratteristiche della risposta transitoria migliorano (questo dovrebbe anche rendere la risposta più rapida). p1 = -20 + 20i; p2 = -20 - 20i; p3 = -100; K = place(A,B,[p1 p2 p3]); lsim(A-B*K,B,C,0,u,t,x0);
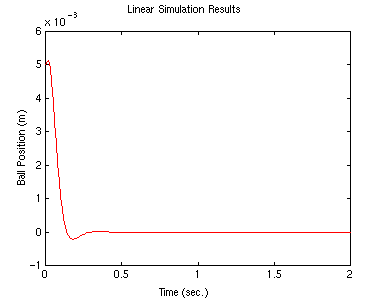
Questa volta l’overshoot è più piccolo: potete consultare il vostro libro di testo per ulteriori suggerimenti su come posizionare i poli per ottenere le caratteristiche richieste. Potete inoltre provare a confrontare il controllo K richiesto nei due casi. In genere comunque, tanto più i poli sono spostati lontano, tanto più grande diventa il controllo K.
Nota: se volete posizionare due o più poli nella stessa posizione, il comando place non funziona, bensì dovete utilizzare il comando acker, che utilizza una sintassi analoga:
K = acker(A,B,[p1 p2 p3])
Introduzione dell’ input di riferimento
Ora prenderemo il sistema di controllo definito precedentemente e vi applicheremo un ingresso a gradino (scegliamo un valore piccolo per il gradino così siamo sicuri di rimanere nel campo di validità della linearizzazione): a questo scopo sostituite t,u e lsim nel vostro M-file con le seguenti righe:
t = 0:0.01:2; u = 0.001*ones(size(t)); lsim(A-B*K,B,C,0,u,t)
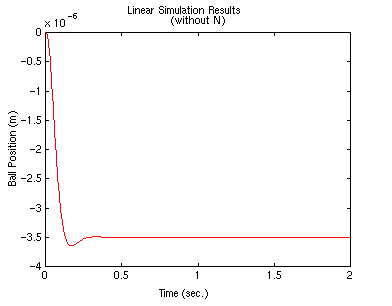
Il sistema non segue per niente bene l’ingresso: non solo l’ampiezza non è unitaria, ma è negativa anziché positiva!
In realtà però noi non stiamo confrontando l’uscita all’ingresso, bensì misuriamo gli stati, li moltiplichiamo per il vettore dei guadagni k e poi sottraiamo questo risultato dal riferimento, ma non c’è motivo di aspettarsi che K*x sia uguale all’uscita desiderata. Per eliminare questo problema possiamo variare l’ampiezza del’input di riferimento per renderlo uguale al K*x in condizioni stazionarie. Questo fattore di scala è spesso chiamato Nbar e viene introdotto come mostrato nel seguente schema:
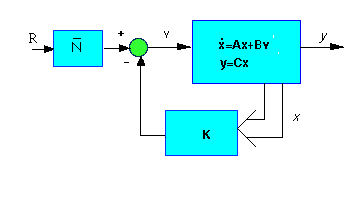
Possiamo ottenere il valore di Nbar utilizzando le formule ricavate a lezione.
Se ora vogliamo calcolare la risposta del sistema con retroazione degli stati utilizzando questo ingresso di riferimento, è sufficiente notare che l’ingresso è moltiplicato per questo nuovo fattore Nbar:
lsim(A-B*K,B*Nbar,C,0,u,t)
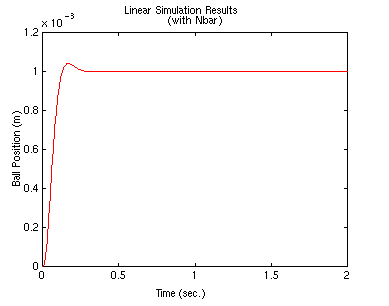
Come si vede ora la risposta allo step viene tracciata ragionevolmente bene.
Realizzazione dell’osservatore
Quando non possiamo misurare tutti gli stati x (come spesso succede), possiamo costruire un osservatore per stimarne il valore misurando solamente l’uscita y = C x. Per la sfera magnetica, ad esempio, aggiungeremo tre nuovi stati stimati al sistema: lo schema sarà il seguente:
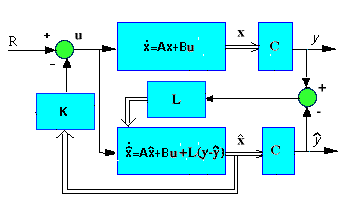
L’osservatore è essenzialmente una copia
del sistema: ha gli stessi ingressi e per lo più le stesse
equazione differenziali. Un termine aggiuntivo confronta le
uscite misurate 
con quelle stimate dell’osservatore; grazie a
questo si può ottenere un valore degli stati stimati
coerente con quello degli
stati effettivi; l’errore dovuto alla dinamica
dell’osservatore è dato dai poli (A-L*C).
Innanzitutto dobbiamo decidere il guadagno L dell’osservatore: poiché vogliamo che la dinamica dell’osservatore sia molto più veloce di quella del sistema stesso, dobbiamo posizionare i poli almeno cinque volte più a sinistra dei poli dominanti del sistema.
Se vogliamo usare il comando place, dobbiamo posizionare i tre poli dell’osservatore in posizioni differenti:
op1 = -100; op2 = -101; op3 = -102;
Grazie alla dualità esistente fra controllabilità ed osservabilità, possiamo usare la stessa tecnica utilizzata per trovare la matrice di controllabilità, sostituendola matrice B con la C e prendendo le trasposte di entrambe le matrici:
L = place(A',C',[op1 op2 op3])';
Le equazioni nel diagramma a blocchi precedente sono date per
.
E’ abitudine scrivere le equazioni combinate per il sistema
e l’osservatore usando lo stato originale x più l’errore sullo stato:
e = x –.
Usiamo invece per gli stati retroazionati u = -K.
Dopo alcuni passaggi algebrici (consultate il vostro libro di testo per questo) si arriva alle equazioni combinate stato ed errore per il sistema con retroazione degli stati ed osservatore:
At = [A - B*K B*K
zeros(size(A)) A - L*C];
Bt = [ B*Nbar
zeros(size(B))];
Ct = [ C zeros(size(C))];
Per vedere com’è la risposta alle condizioni iniziali non nulle senza ingresso di riferimento, potete aggiungere le seguenti linee nel vostro M-file; si assume generalmente che l’osservatore parta con condizioni iniziali nulle.
=0
Ciò comporta che le condizioni iniziali dell’errore siano pari alle condizioni iniziali dello stato:
lsim(At,Bt,Ct,0,zeros(size(t)),t,[x0 x0])
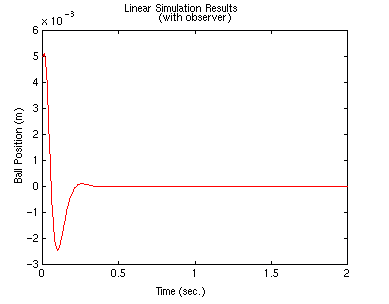
Le risposte di tutti gli stati sono plottate qui di seguito:
ricordate che lsim ci fornisce x ed e; per ottenereè necessario calcolare x-e.
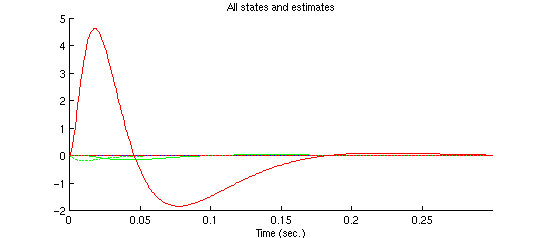
Possiamo fare uno zoom per vedere meglio i dettagli:
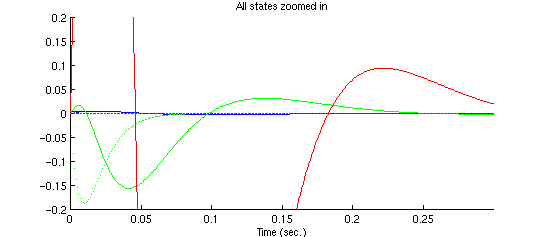
La linea continua blu è la risposta per la posizione della sfera
La linea tratteggiata blu è lo stato stimato
La linea continua verde è la risposta per la velocità della
sfera 
La linea tratteggiata verde è lo stato stimato
La linea continua rossa è la risposta per la corrente
La linea tratteggiata rossa è lo stato stimato
Possiamo vedere che l’osservatore stima gli stati velocemente e ne traccia la risposta ragionevolmente bene nello spazio dehli stati: i grafici sopra riportati possono essere ottenuti con il comando plot.
Forma il regolatore del sistema partendo dalle matrici di stato, dalle matrici del controllore sugli stati e dall'osservatore.
Partendo da un sistema nella forma
d x/dt = Ax + Bu , y = Cx + Du
Il regolatore risultante sarà:
d(x_e)/dt = [A-BK-LC+LDK] x_e + Ly
u = -K x_e
L'istruzione da utilizzare è la seguente:
RSYS = REG(A,B,C,D,K,L)
Una volta ottenuto il regolatore è possibile retroazionarlo con il sistema da controllare utilizzando l'istruzione feedback.
Permette di ottenere la matrice di controllabilità, con l'utilizzo dell'istruzione:
CO = CTRB(A,B)
che equivale quindi al calcolo di: [B AB A^2B ...]. E' necessario, successivamente, verificare che la matrice ottenuta abbia un determinante non nullo (o il rango pari al numero degli stati) perchè il sistema sia controllabile.
Permette di ottenere la matrice di osservabilità, con l'utilizzo dell'istruzione:
OB = OBSV(A,C)
che equivale quindi al calcolo di [C; CA; CA^2 ...]. E' necessario, successivamente, verificare che la matrice ottenuta abbia un determinante non nullo (o il rango pari al numero degli stati) perchè il sistema sia osservabile.